0x01契机
一直没有机会也没下定决心认真的去研究某个安全领域，很早之前就看到好多人研究RFID，一直很憧憬那片天空，趁着老大给机会，决定选这个方向作为个人业余努力的方向。 差不多四天前入手了ACR122U，决定拿自己母校的餐厅饭卡练手。 ACR122U的使用很简单，只要安装上驱动，使用M1卡服务程序就可以很快破解，破解完成后查看其生成的dump文件，找到加密扇区的密码，将密码导入到MCT (Mifare Classic Tool)，剩下的就可以完全使用MCT完成了，个人很怀疑破解过程是否完全可以通过手机（支持NFC）APP完成。ACR122U的详细使用过程可以参考：RFID安全之某学校水卡破解，本文主要介绍目前M1卡中的数据分析和M1卡安全防护方案。
0x02背景知识
了解M1卡的结构可以知道M1卡共16个扇区，编号从0到15，每个扇区配备了从0到3共4个段，每个段可以保存16字节的内容。
0x03数据分析
阅读《RFID安全之某学校水卡破解》可以发现该学校的水卡中数据存储比较简单，按照作者的分析，4号扇区的1、2号数据段（编号从0开始）存储了水卡余额，将已知的余额32.31，换算为分为3231，再转为16进制为C9F，即00000C9F，而0C9F取反为FFFFF360，这时比较下4号扇区的值，很容易发现规律：前四个字节不取反倒序（9F0C0000）存储余额，接下来四个字节取反倒序（60F3FFFF）存储余额，再接下来四个字节不取反倒序（9F0C0000）存储余额。
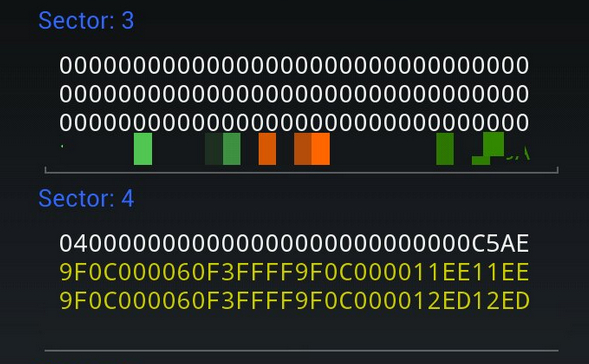
上面提到的“倒序”，可以结合计算机数据存储方式来理解：如下图所示，变量a存储的数据对应的16进制为0A112233，变量b存储的数据对应的16进制为0B445566。
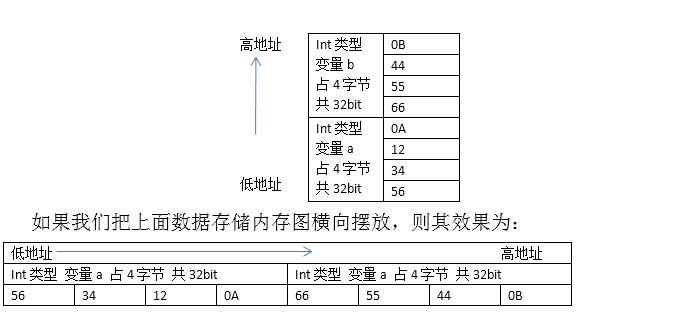
这样就很明显了，5634120A，就是变量a所代表的数据的十六进制0A123456的倒序。 作为入门教程，个人认为《RFID安全之某学校水卡破解》是非常不错的。看完这个教程，并实践结束后，我停下来思考这样一个问题：M1卡的密码破解是傻瓜式的，当然也有文章介绍破解原理，但是作为门外汉，目前我还不是特别关心，我只想找到那种破解成功，可以修改金额的快感！那么在整个M1卡的破解过程中，我自己到底起了什么作用？答案是卡片的数据分析。 《RFID安全之某学校水卡破解》中的数据分析并不难，只要知道水卡的余额就可以定位卡片中余额数据的存储位置，细心的读者肯定可以发现文中的截图5号扇区也存在非0值块，作者在《RFID安全之某学校水卡破解后记——不留后患》中作了进一步分析；《任意修改学校食堂饭卡余额》这篇文章所描述的卡片和《RFID安全之某学校水卡破解》的分析非常相似；而另一篇《破解学校水卡-–||||RFID Hack初探 》文中的数据就更简单了，只有余额和消费金额之和，连取反的校验都没做。 分析了几篇图文教程式入门文章，加上自己的实际破解过程，总结了一下数据分析的经验。 首先，需要收集信息，然后可以通过数据比对法定位余额，如果卡片数据采取了校验保护，可以采用试错法进行排查定位，正如《RFID安全之某学校水卡破解后记——不留后患》中所用到的方法。
0x03.1比对法
比对法，就是将已知数据换算成十六进制，寻找卡片中能与之对应的数据，从而确定卡片中对应的存储位置所存储的数据的意义，或者将卡片中变化的字节转成十进制，判断是否存在相应的数据信息。 最常用的比对值当然是卡片余额，还有当前的消费金额，或者是累计的消费金额，这两个数据有出现在前文的引用文中。那么除了这些，还应该考虑哪些数据呢？这里我作一个简单的罗列：消费次数、日期、时间、读卡器编号、卡号（非UID）等 之所以认为上面的数据可以存储在卡片中，是因为两个字节（16bit），不考虑符号位，可以表示的最大数值是65535，一个字节（8bit）可以表示最大数值为255。一张卡按四年有效期来算的话，每天要刷44次才能再四年内超过这个数值；日期也可以用两个字节来表示，可以选择整体表示，譬如12月31日，记为1231，对应到16进制04CF，也可以一个字节表示月一个字节表示日，仍然是12月31日，可以记为0C1F（1F=31）；时间（不考虑秒）的最大表示数字是23:59，也可以参考日期的表示方式，选择不同的方案；读卡器编号，一般情况下一个单位也不会同时具有65535台读卡设备；卡号，这里卡号一般可以用两个字节表示，如果单位人数较多（超过65535），也可以使用四个字节表示，卡号的意义可以标识一个人，也可以标识单位内的一个部门等。
0x03.2试错法
试错法就是针对一些不明意义的字节（可能是校验字节），通过修改已知意义的字节来确定其关联性，找出不明意义字节的计算方法。 数据比对法，有时并不能分析出所有数据块的数据，这时可以考虑试错法来确定隐晦数据和哪些字段有关联，譬如下面的案例： 卡片只有0号扇区有数据：
43 9A ** ** ** ** 04 00 46 BA 14 12 51 10 03 10 第0段
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
11 01 ** ** ** ** FF 07 80 69 FF FF FF FF FF FF 第3段
第0段为厂商写死的UID，不可修改，经过多次信息收集发现第1段的数据是不变的，变化的只有第二段，经过比对法，发现第1段的4A 3D是卡号，第2段的01 C2是本次消费金额，0E A6是余额，027D是消费和充值次数，081D是日期，到此，第2段中还有前四个字节以及最后两个字节的意义不明。 下面通过试错来定义各个字节的意义 尝试直接修改K1余额，读卡会失败，于是认为刷卡消费过程存在验证，余额和消费金额并不能构成验证对，所以认为验证信息在意义不明的6个字节内。 只修改消费金额也会导致读卡失败。 尝试使用K2的值整体替换K1的第2段，结果读卡依然失败。 最后尝试使用K2的值，整体替换K1的第1和第2段，等价于复制卡片，终于读卡成功了。 通过以上几步，可以确定消费读卡器在进行扣钱之前，会先校验卡片的正确性，校验值和余额、消费金额以及第1段中的数据都有关联。为了进一步定位信息，做出如下试错计划：
1、修改卡号，确认卡片是否可正确识别； 2、逐个修改第2段中已知意义的字节，确认卡片是否可正确识别，排除与校验无关的字节 3、对第2段中不明意义的6个字节逐个修改，确认卡片是否可正确识别，排除非校验字节 4、对第1段中的3个不明意义的字节逐个修改，确认卡片是否可正确识别 本质是就是对所有数据字节进行试错，排除与校验无关的字节！ 通过以上过程缩小与校验相关的字节，再结合比对法中找出的已知意义的字节，从而确定不明意义字节的意义和校验算法。 由于刷卡条件限制，以上案例尚未破解完成，试错法也有待该案例进一步验证。 破解过程需要大胆猜测，努力求证！
0x04卡片防护
破解和防护是一对冤家，既然M1卡这么容易被破解，那有没有合适的防护方法呢？上一小节中提到的校验案例就算是一个很小的防护手段，但是依然存在很大被破解的风险。 为了降低水卡和饭卡被破解的风险，同时又不增加替换M1卡的成本，可以完全加密数据字段，基于密钥和算法保密性，保证即使可以通过验证攻击获取到M1卡中的数据，黑客也无法快速判断各个数据字段的意义，从而无法完成余额修改！ 譬如，参考上一小节的校验案例，如果所有数据再与一个2字节的密钥进行异或处理，这时就无法简单的通过比对法判断出哪些字节是余额、哪些是消费金额，进一步降低了破解风险。当然针对密钥可以设计一套动态密钥方案，效果类似支付宝令（需要考虑如何处理长期不使用的卡片），而加密算法可以选择更加复杂的对称加密算法，只要保证不会对消费刷卡机造成过大延迟即可。
0x05复制攻击
数据加密虽然可以增加黑客分析卡片数据的难度，降低黑客恶意修改余额的风险，但是无法应对卡片复制攻击！ 复制攻击可能造成的后果是盗刷他人饭卡或水卡，这一点是最容易理解的，当然前提是黑客可以接触到别人的饭卡或水卡。 除了这一点，复制攻击是否还存在其它危害？ 在分析这之前，需要明确几个前提，1）刷卡机中会记录哪些信息；2）我们假设刷卡机没7天向中央数据库服务器提交一次数据，刷卡机向中央数据库提交的是哪些数据。 如果刷卡机只记录一张卡片的最后一次消费记录，那么其向数据库提交的数据必然要包含余额信息。如果在刷卡机两次向数据库提交数据的时间间隔内，利用复制的卡片（复制较早的卡片数据）做最后一次消费，那么真实卡片消费的数据就会被覆盖掉。 当然个人猜测目前的刷卡机应该会记录卡号（非UID）、消费累计金额、消费次数，同步数据库时只需要基于卡号找到对应的记录，然后将余额减去消费累计金额、总消费次数叠加本次提交的消费次数。这种情况下，复制攻击就只能盗刷他人的饭卡或水卡余额了，但是即使是这样，如果不影响被复制的卡，也算是一种修改余额的方式，毕竟刷卡机不会基于数据库信息向卡片写数据！ 本来以为复制攻击就这些影响了，晚上睡觉前忽然想到，既然可以复制别人的卡，为什么不能复制自己的卡呢。T1时间充值m元，并记录下卡内的数据信息D1，消费一段时间后，T2时间卡内余额n元（n<m），此时将数据信息D1重新拷贝回卡内，卡片信息重新回到T1时间的状态，等价于T1-T2时间段内没做任何消费！这种情况即使是使用UID作校验也无法防护了，除非刷卡机是在线实时查询数据库的，后来发现这种攻击方式12年就有人提出了，并称之为重放/重置攻击。
0x06后记
刚接触RFID，有描述不准确或错误的地方，请轻拍指正！
0x07卷土再来
基于0x05节的分析和实际验证，通过复制攻击（重放攻击）已经实现0x03.2节示例中卡片的余额修改，但是为了论证 0x03.2节试错法的可行性，规划了如下方案：
43 9A ** ** ** ** 04 00 46 BA 14 12 51 10 03 10 第0段
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
11 01 ** ** ** ** FF 07 80 69 FF FF FF FF FF FF 第3段
针对以上信息，对第1、2段内容，逐字节进行试错，确认卡片是否可读 验证结果如下： 1、修改第1段第0字节
0D 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
2、修改第1段第1字节
0C 0E 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
3、修改第1段第2字节
0C 0D 0D 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
4、修改第1段第3字节
0C 0D 0C 12 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
5、修改第1段第4字节
0C 0D 0C 11 01 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
6、修改第1段第5字节
0C 0D 0C 11 00 01 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
7、修改第1段第6字节
0C 0D 0C 11 00 00 4B 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
8、修改第1段第7字节
0C 0D 0C 11 00 00 4A 3E 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
9、修改第1段第8字节
0C 0D 0C 11 00 00 4A 3D 01 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
10、修改第1段第9字节 0C 0D 0C 11 00 00 4A 3D 00 2E 00 00 00 01 00 47 第1段 37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
11、修改第1段第10字节 0C 0D 0C 11 00 00 4A 3D 00 2D 01 00 00 01 00 47 第1段 37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
12、修改第1段第11字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 01 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
13、修改第1段第12字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 01 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
14、修改第1段第13字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 02 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
15、修改第1段第14字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 01 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
16、修改第1段第15字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 48 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
17、修改第2段第0字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
38 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
18、修改第2段第1字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0C BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
19、修改第2段第2字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BD E4 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
20、修改第2段第3字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E5 01 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
21、修改第2段第4字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 02 C2 00 00 0E A6 02 7D 08 1D 05 60 第2段
22、修改第2段第5字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C3 00 00 0E A6 02 7D 08 1D 05 60 第2段
23、修改第2段第6字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 01 00 0E A6 02 7D 08 1D 05 60 第2段
24、修改第2段第7字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 01 0E A6 02 7D 08 1D 05 60 第2段
25、修改第2段第8字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0F A6 02 7D 08 1D 05 60 第2段
26、修改第2段第9字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A7 02 7D 08 1D 05 60 第2段
27、修改第2段第10字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 03 7D 08 1D 05 60 第2段
28、修改第2段第11字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7E 08 1D 05 60 第2段
29、修改第2段第12字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 09 1D 05 60 第2段
30、修改第2段第13字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1E 05 60 第2段
31、修改第2段第14字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 06 60 第2段
32、修改第2段第15字节
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
37 0B BC E4 01 C2 00 00 0E A6 02 7D 08 1D 05 61 第2段
本来期望可以得到一个很不错的结果的，甚至连测试结果位置都预留了，天不遂人愿，畏畏缩缩的在一个窗口连刷了32次，每次都是读卡失败，这下郁闷了，本以为破解只能止步于此了。 又拖了一周，感觉自己都没激情了，只是偶尔抽时间看看之前收集的数据，却总结出了下面的结果：
13 05 71 22 04 E2 00 00 01 54 03 15 08 19 0D FC 0E0E
13 05 71 22 27 10 00 00 28 64 03 16 08 19 0D 37 0404
59 04 71 96 04 E2 00 00 23 82 03 17 09 01 0D EC 6767
13 05 86 B3 04 E2 00 00 1E A0 03 18 09 02 0D 66 E7E7
13 05 89 8E 01 90 00 00 1D 10 03 19 09 03 04 99 E7E7
13 05 92 5C 04 E2 00 00 18 2E 03 1A 09 04 0D 11 F5F5
59 04 78 53 03 52 00 00 14 DC 03 1B 09 05 09 F2 3535
注：这是另一张卡上收集的数据，两个字节两个字节进行异或运算再与始终不变的第1段逐两字节异或 开始时，始终没能搞清楚这个异或结果，今天突然想到，每两个字节进行异或的结果出现的是两个相同的字节值，那么逐个字节异或岂不就是0，经此确认，试错法终于可以再次登场了，结合之前的32次试错，大胆猜测卡片的校验过程：第1和第2段逐字节异或为0。 现在明确了卡片关键的两段数据逐字节异或为0的校验条件，再次进行如下试错测试： 前提：当前卡片数据（消费读卡器可识别）
43 9A 5D A7 23 88 04 00 46 BA 14 12 51 10 03 10 第0段
0C 0D 0C 11 00 00 4A 3D 00 2D 00 00 00 01 00 47 第1段
26 02 99 63 01 2C 00 00 0D 7A 02 7E 08 1F 03 EC 第2段
11 01 08 46 04 20 FF 07 80 69 FF FF FF FF FF FF 第3段
1、尝试修改第一段中的数据
1.1 4A3D-->5324 结果：不可读
1.2 4A3D-->4A3E 0047-->0044 结果：可读
2、修改第二段中的数据 2.1修改第二段中的最后两个字节：
03EC-->00EF 结果：可读
2.2修改第二段中最前面的两个字节：
2602-->2400 结果：可读
2.3修改第二段中第三四个字节：
9963-->966C 结果：可读
2.4整段替换第二段：
26 02 99 63 01 2C 00 00 0D 7A 02 7E 08 1F 03 EC3-->13 05 86 B3 04 E2 00 00 1E A0 03 18 09 02 0D 66
结果：可读，金额变化一致；却与之前的一次实验结果冲突！
通过上面的试错，基本可以明确针对第2段的校验过程：逐字节异或，判断结果是否为0。为进一步验证猜测，构造如下数据：
1E 02 66 83 02 3C 00 00 EF C4 03 FF 08 FF 03 E4
这条人为构造的数据，余额为613.8元，消费金额为5.72元，消费日期为一个不存在的日期，如果该该数据能够校验通过，那么破解基本就可以结束了。 1E 02 66 83 02 3C 00 00 EF C4 03 FF 09 1E 03 04，如果上一条不能成功，则尝试该日期正确的数据。 经过验证，随意构造的两条数据都成功修改了卡片余额，如下图：
到此，卡片的破解算是告一段落，虽然遗留了一下问题： 1、整体替换两次实验结果冲突？ 2、第2段中的前四个字节以及最后两个字节的数据是如何产生的？ 第一个问题可能是自己粗心造成的；第二个问题并不影响卡片破解。
0x08小结
通过上面的实例分析，再次总结卡片破解过程中数据分析的两大步骤： 1、数据比对 收集多组数据，结合消费金额、余额、日期、消费次数等已知信息确定数据段中各个字节的含义 2、试错分析 在直接修改余额出错的情况下，逐字节或整体试错，确定校验相关字节，并猜测校验算法，一般情况下，校验算法是可逆算法，字节运算一般主要考虑异或运算；然后通过试错进行论证；最后自己构造数据实现卡片余额修改，完成破解。
云悉指纹